Please click the videos for better view.
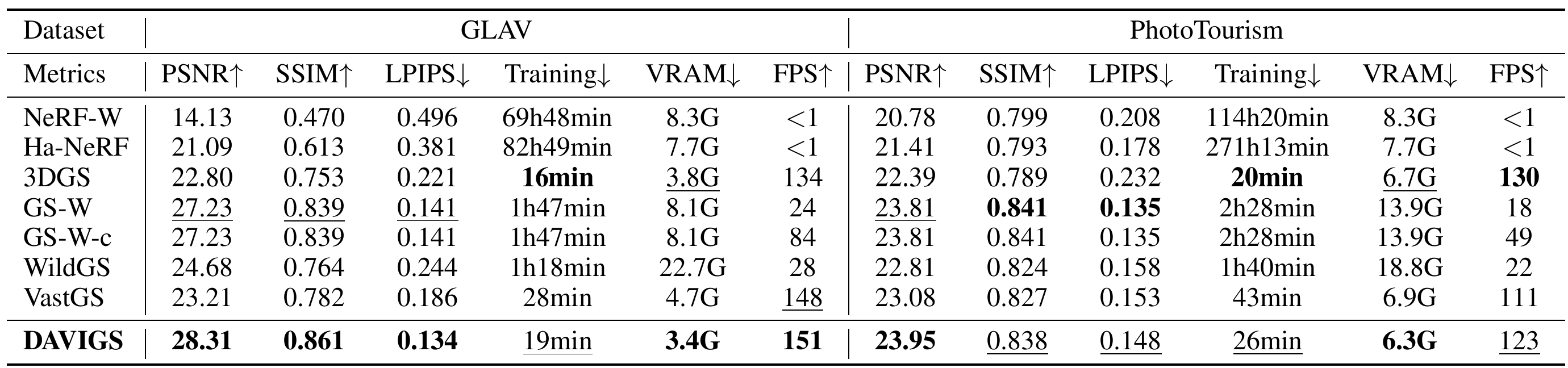
Abstract
Gaussian Splatting has emerged as a prominent 3D representation in novel view synthesis, but it still suffers from appearance variations, which are caused by various factors, such as modern camera ISPs, different time of day, weather conditions, and local light changes. These variations can lead to floaters and color distortions in the rendered images/videos. Recent appearance modeling approaches in Gaussian Splatting are either tightly coupled with the rendering process, hindering real-time rendering, or they only account for mild global variations, performing poorly in scenes with local light changes. In this paper, we propose DAVIGS, a method that decouples appearance variations in a plug-and-play and efficient manner. By transforming the rendering results at the image level instead of the Gaussian level, our approach can model appearance variations with minimal optimization time and memory overhead. Furthermore, our method gathers appearance-related information in 3D space to transform the rendered images, thus building 3D consistency across views implicitly. We validate our method on several appearance-variant scenes, and demonstrate that it achieves state-of-the-art rendering quality with minimal training time and memory usage, without compromising rendering speeds. Additionally, it provides performance improvements for different Gaussian Splatting baselines in a plug-and-play manner.
Method

Overall pipeline of DAVIGS. For each pixel $p$ in the rendered image $\mathcal{I}^r$, we calculate its 3D spatial position $\mathbf{x}$ by back-projecting with its depth $\mathcal{D}(p)$ in the depth map $\mathcal{D}$, and then look up the multi-resolution hash grids for its 3D consistent features $\{\mathbf{f}_i\}$. They are then concatenated with a view-dependent appearance embedding $\mathbf{l}$ and fed into an MLP $f$ to obtain a transformation matrix $\mathcal{M}(p) \in \mathbb{R}^{3\times 4}$, which is used to perform affine transformation on the color $\mathcal{I}^r(p)$ to obtain $\mathcal{I}^t(p)$. The losses $\mathcal{L}_1$ and $\mathcal{L}_\text{D-SSIM}$ are calculated between the transformed image $\mathcal{I}^t$ and the ground truth image $\mathcal{I}$. A regularization term $\mathcal{L}_\mathrm{ID}$ is applied to $\mathcal{M}(p)$ for constraining it close to the identity transformation matrix $\mathcal{M} _{\mathrm{ID}}$.